Runge Kutta方法求解微分方程

普通的常微分方程已经有成熟的各类方法进行求解，而且得到的是解析解的形式。不过对于在计算机上求解而言，符号运算编程的难度可能要超过数值运算编程，所以，直接寻求数值解在某些情况下可能更加方便。欧拉方法和龙格库塔方法就是常见的数值计算方法。 将一阶常微分方程初值问题写成如下形式： \[\left\{\begin{array}\~y^{'}=f(x,y) \\y(x_0)=y_0 \\ \end{array}\right.\] 四阶Runge Kutta公式如下： \[\left\{\begin{array}{l}y_{n+1}=y_n+\frac{h}{6}(K_1+2K_2+2K_3+K_4)\\x_{n+1}=x_n+1\\K_1=f(x_n,y_n)\\K_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_1)\\K_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}K_2)\\K_4=f(x_n+h,y_n+hK_3)\end{array}\right.\] 四阶Runge Kutta公式在实际应用时精度较高（4阶精度）而且计算量适中，因此使用较多。 对于求解微分方程组，可以将方程组写成向量形式，这样上面的4阶Runge Kutta公式不需要改变形式，只要把四个参数改成相应的向量形式即可。求解高阶微分方程则可以通过降维方式令\(y^'=x,y^{''}=x^'\)就可以转化为一阶微分方程组的形式。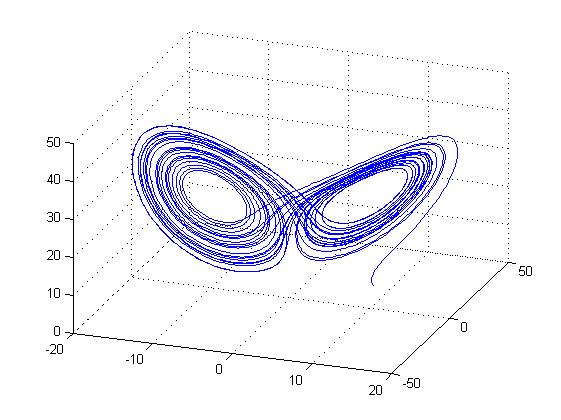 利用4阶RK方法求解洛伦兹方程： \[\left\{\begin{array}\frac{dx}{dt}=\sigma(y-x)\\ \frac{dy}{dt}=x(\rho-z)-y\\ \frac{dz}{dt}=xy-\beta~z\end{array}\right.\]取\(\sigma=10,\beta=\frac{8}{3},\rho=28\)。相空间轨迹如下图：

% By voidmous
% 利用四阶Runge Kutta求解洛伦兹方程
clear all;close all;clc
h=0.005; n=30/h+1; sigma=10;beta=8/3;rho=28;
y=zeros(3,n); t=zeros(1,n); y(1,1)=10; y(2,1)=3; y(3,1)=5;
f=inline('[sigma\*(y-x);x\*(rho-z)-y;x\*y-beta\*z]','x','y','z','sigma','beta','rho');
for i=2:n
k1=f(y(1,i-1),y(2,i-1),y(3,i-1),sigma,beta,rho);
k2=f(y(1,i-1)+h\*k1(1,1)/2,y(2,i-1)+h\*k1(2,1)/2,y(3,i-1)+h\*k1(3,1)/2,sigma,beta,rho);
k3=f(y(1,i-1)+h\*k2(1,1)/2,y(2,i-1)+h\*k2(2,1)/2,y(3,i-1)+h\*k2(3,1)/2,sigma,beta,rho);
k4=f(y(1,i-1)+h\*k3(1,1),y(2,i-1)+h\*k3(2,1),y(3,i-1)+h\*k3(3,1),sigma,beta,rho);
y(:,i)=y(:,i-1)+h\*(k1+2\*k2+2\*k3+k4)/6;
t(i)=t(i-1)+h;
end
%静态显示洛伦兹变化轨迹 plot3(y(1,:),y(2,:),y(3,:)) view([20,32]);
grid on %动画显示绘制过程 %暂时无法调整视角，也许看comet绘制原理有用？
%comet3(y(1,:),y(2,:),y(3,:))

[1]Wikipedia contributors. Runge–Kutta methods[J]. Wikipedia, the free encyclopedia, Wikimedia Foundation, Inc., 2012.

[2]Simulation of Lorenz ’63 model: 4th order Runge-Kutta[M]. 2010.

[3]魏诺. 非线性科学基础与应用[M]. 科学出版社, 2004.

[4]Wikipedia contributors. 龙格－库塔法[J]. 维基百科，自由的百科全书, Wikimedia Foundation, Inc., 2012.

[5]洛伦兹方程的matlab求解_百度文库[EB/OL]. [2012-05-01]. http://wenku.baidu.com/view/169b50c7aa00b52acfc7ca50.html.